Very Far From Home: The James Webb Space Telescope

The James Webb Space Telescope (JWST) just launched about a week ago, on Christmas Day 2021.  Its final destination: Lagrange Point number 2 (called “L2”).  This is four times farther from Earth than the Moon, effectively rendering JWST unreachable by astronauts (at least with current and near-future spacecraft technology) for maintenance and refueling.  In this article I’d like to explore why the decision was made to do this and what some of its consequences are.

The Earth-Sun system has five Lagrange Points (labeled L1 through L5).  At these five Lagrange Points, the inward pull of gravity exactly balances the outward push of the centrifugal force. Let’s explore this idea.

Centrifugal Forces and Rotating Reference Frames

Let’s start with an example. You’re riding in a seat on the right side of a car and the car turns left. You feel yourself pushed towards the outside edge of the vehicle while the car turns. You just experienced the centrifugal force.

But wait, as you may remember if you took high school physics, the centrifugal force is a “fictitious force”, right?  That’s true; it only appears because we are doing physics in a rotating (e.g., turning) reference frame (more on that in a minute).  Take away the rotating reference frame and the centrifugal force disappears.

However, despite the unfortunate naming convention for fictitious forces, this doesn’t mean the centrifugal force is unreal.  You verify this yourself every time you experience the situation in the above example: when you are pushed towards the outer edge of a car while it’s turning, that feels pretty real, right?  And it is.

As another example, centrifuges use the centrifugal force to separate objects of different mass density (i.e., different inertia). And centrifuges work just fine!

The centrifugal force is called fictitious because there isn’t actually something pushing you towards the car door.  The centrifugal force arises as a result of your inertia.

As Newton’s First Law tells us, an object in motion will continue moving in a straight line and at the same speed until acted on by a force.  Let’s consider again the situation where you’re riding in a car that turns left, this time as viewed by a third party that’s outside the car. They would see your body and the car are moving forward in a straight line.  When the car curves left, your body wants to continue moving in the direction the car was originally traveling, but the car forces you to go left. When it does so, you feel like you are moving towards the car door. Actually, when viewed from outside the car, we can see that the car door moved towards you.

To summarize so far: if we take the world outside the car to be the reference frame, we are able to see that the passenger wants to go in a straight line but is coerced into turning left by the car.

But now let’s look at this again, taking the car to be your reference frame.  This is perhaps easier to visualize if you imagine there are no windows in the car and the only thing you can see is the interior of the car.  In this reference frame, everything in the car is at rest with respect to you (i.e., the dashboard, doors, and seats are all staying at a constant distance from you). When you feel the centrifugal force “push” you toward one door, it’s because your reference frame — the car — moved (actually, it accelerated). But to you it appears as if you moved, since the car’s interior is your reference frame. In other words, if the interior of the car consists of all objects that are at rest, then it appears that something pushed you closer to the door.

Because fictitious forces arise due to inertia, they are sometimes — and more appropriately — called “inertial forces”.

One can also see that if the car weren’t turning there would be no centrifugal force for the person inside the car.  And this is the idea behind why the centrifugal force disappears if the reference frame isn’t rotating (e.g., turning). (Aside: the coriolis force is another fictitious/inertial force that arises when you’re in a rotating reference frame; it applies to the Sun-Earth system as well).

One more example of the centrifugal force is the force you feel when riding on a merry-go-round. The merry-go-round is your rotating reference frame. You have to hang on to the merry-go-round to avoid flying off. The sensation of the centrifugal force is caused by your inertia, which wants you to move in a straight path (and fly off the merry-go-round) instead of a curved path (and stay on the merry-go-round). So you have to hold on in order to fight your inertia (i.e., the centrifugal force) and stay on the merry-go-round. You may also be able to imagine that as you move closer to the center (axis of rotation) of the merry-go-round, it becomes easier to hold on. And as you move closer to the edge of the merry-go-round, it becomes harder to hold on. All of this applies equally well to planets orbiting the Sun.

Mathematical aside: The formula for centrifugal force is , where is your mass, is how fast the merry-go-round (i.e., the reference frame) is spinning, and is your radial position (i.e., how far you are from the center). As the merry-go-round spins faster ( increases), it gets much harder to hold on (since the centrifugal force is proportional to the square of ). As you move toward the center ( gets smaller), gets smaller and therefore it becomes easier to hold on; and conversely, if you move toward the edge ( gets larger), gets larger and therefore it becomes harder to hold on. End mathematical aside

In the case of the Sun-Earth system, the rotating reference frame is the one in which the Sun and Earth are at rest (just as you were at rest with respect to the interior of the car). If we add a third object to the Sun-Earth system (such as the Moon, or an artificial satellite such as the International Space Station or JWST), we are now considering the famous three-body problem.

The three-body problem is unsolvable in the general case, but in certain special cases it has been solved, famously by Euler and Lagrange. For instance, it is solvable by considering a special case called the restricted three-body problem, in which the first two objects (e.g., the Sun and Earth) have a large gravitational influence and the third body (such as a spacecraft or the Moon) doesn’t contribute much to the gravitational field but instead is like a “passenger” that only “surfs” on the gravitational field, without altering it.

In 1767, by studying the three-body problem through mathematics alone, Euler discovered L1 through L3.

And in 1772, also studying the three-body problem again through mathematics alone, Lagrange discovered L4 and L5.

So what exactly are L1 through L5?

Lagrange Points

The centrifugal force is present for the Earth because it is in the rotating reference frame of the Sun-Earth system, just as the centrifugal force is present when we’re in the reference frame of a car as it makes a turn, or in the reference frame of a merry-go-round as it spins.

At a Lagrange Point, the centrifugal force cancels with the gravitational forces from the Sun and Earth. Therefore an object sitting at a Lagrange Point will remain “at rest” since there is no net force. Being “at rest” in this frame means the object isn’t moving closer or farther from the Earth and Sun. However, it is still orbiting the Sun since the reference frame itself is spinning.

This is entirely analogous to the merry-go-round, except instead of us holding on with our hands, gravity is the force holding things in orbit. The gravitational pull towards the Sun balances against the centrifugal force and therefore the Earth doesn’t go flying off its “interplanetary merry-go-round”.

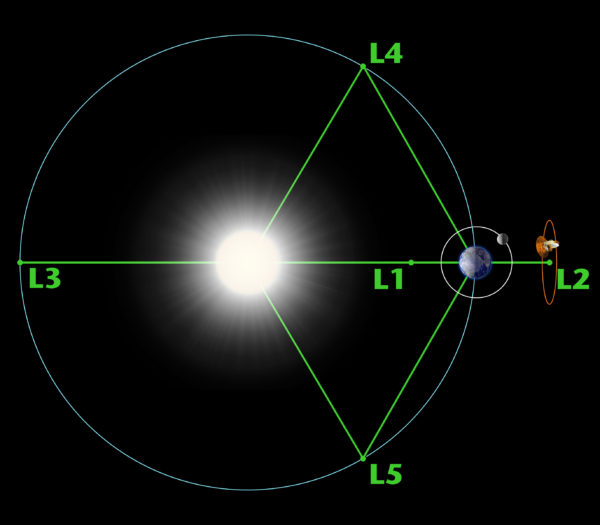
Image credit: wikimedia commons

Of the five Lagrange points, three (L1, L2, and L3) lie along the straight line connecting the Earth and Sun (see image).

L1 is between the Earth and Sun.  At L1, the inward pull of the Sun’s gravity is exactly balanced by the outward pull of the Earth’s gravity combined with the outward centrifugal force.

L2 lies on the same line connecting the Sun and Earth, but outside Earth’s orbit.  L2 makes an orbit around the Sun in lock-step with the Earth, but its orbit is an extra 1.5 million km farther from the Sun than Earth is.  At L2, the Sun and the Earth are both pulling inward with gravity (this time working in the same direction and therefore adding together) and that is balanced by the outward centrifugal force (which is larger for larger orbits, just as its harder to hang on the merry-go-round as you move farther from the center).

L3 occupies a spot on the opposite side of the Sun from the Earth like a mirror image of the Earth, orbiting the Sun in the same orbit and always opposite to the Earth.

L4 and L5 also orbit the Sun along the same orbital trajectory as the Earth, one of them (L4) leading the Earth in its orbit and the other (L5) trailing the Earth.

Stable and Unstable Equilibria

All five Lagrange Points are equilibrium points; since the forces there cancel, if you put an object at a Lagrange point it will stay there as it orbits around the Sun.  This makes Lagrange Points a natural choice as locations for putting satellites.

But there’s an added wrinkle.  Of the five equilibrium points, only two (L4 and L5) are stable.

A stable equilibrium is one where, if something nudges the object away from that equilibrium point, the forces that are present will tend to restore equilibrium by pushing the object back toward the equilibrium position.

An example of this is a marble sitting at the bottom of valley on a marble track.  It’s at rest and in equilibrium (i.e., it stays at rest).  If you nudge the marble in either direction, upward from the bottom of the valley, it will naturally roll back towards the bottom of the valley. Therefore it tends to roll back towards its equilibrium point. And that natural tendency to restore equilibrium makes this a case of a “stable equilibrium”.

In cases without much friction, the restoring force that brings an object back to the equilibrium position will cause the object to overshoot the equilibrium position. But once past it, the restoring force will switch directions and work to bring it back towards equilibrium. In this way, you often see an object oscillating back and forth around an equilibrium point (like pendulum) or, in the case of two-dimensional motion, orbiting around the equilibrium point. In the marble track analogy, you can imagine the marble rolling back down toward the valley, gathering speed which causes it to pass through the bottom of the valley and roll up the other side of the track. Then it changes direction and rolls back down to the valley and back up the original side where it started. If the track is frictionless, this would go on forever and the marble would oscillate around the equilibrium point at the bottom of the valley, just like a pendulum swinging back and forth.

An unstable equilibrium is the opposite: if an object is nudged away from its equilibrium point, it will continue moving ever farther from its equilibrium point.  This is analogous to the marble sitting at the top of a peak on the marble track.  Sitting still at the top of the peak it is both at rest and in equilibrium (i.e., it stays at rest).  However, if you nudge it in either direction, it will roll down the hill, getting farther from its equilibrium point and actually accelerating away from equilibrium.

A stable equilibrium point like L4 or L5 might seem like a natural choice for placing an artificial satellite, since the satellite won’t stray far from that equilibrium position.  However, stability is a double-edged sword.  Because of their stability, L4 and L5 tend to be a repository for many natural objects too, like rocks and dust.  Putting a satellite or telescope at L4 or L5 would subject it to possible collisions with other objects. So L4 and L5 are already too crowded with potentially dangerous space rocks.

The James Webb Space Telescope and L2

Wanting to avoid dangerous space debris leaves the less stable Lagrange points L1 through L3 for consideration.  And of those, NASA has selected L2 for JWST.  Actually, JWST will be orbiting around L2 (similar to the marble on the track oscillating around the bottom of the valley, albeit around an unstable equilibrium point instead of a stable one).  JWST’s orbit around L2 is nicely illustrated in the image below and the animation below that.

JWST orbiting L2 (image from solarsystem.nasa.gov)

It will take JWST about a month before it reaches its final position orbiting around L2.

Since L2 isn’t stable, this means JWST will need to course correct periodically (about once every three weeks) in order to remain in orbit around L2.  This requires fuel.  And, as mentioned in the first paragraph, L2 is too far away for astronauts to access it for refueling.

This puts an absolute time limit on JWST’s mission.  Once it’s out of fuel, it can no longer course correct. And it can’t be refueled, therefore that will be the end of its mission.  The life expectancy for JWST’s mission is 5 to 10 years.

Why L2?

Within weeks of Hubble’s launch in 1990, it became infamous for having a mirror flaw that prevented it from taking clear images.  NASA drew criticism from politicians and Hubble became the butt of jokes in popular media, for instance by being compared with other disasters, such as the Titanic, in the comedy movie The Naked Gun.

Hubble wasn’t abandoned, however, and in 1993 astronauts repaired the telescope during a space walk.  Hubble would go on to have decades of use, continues to be used to this day, and is expected to last about another 10 years, ultimately making countless contributions to our understanding of the universe.

The James Webb Space Telescope is a successor to Hubble. Unlike Hubble, however, a repair mission won’t be possible with JWST if something goes wrong.  It is too far away (at least with current and near-future spacecraft technology).  Right now we are waiting with held breath that everything works as planned, since we only get one chance at this mission.

Given that putting JWST at L2 puts it out of reach for maintenance and refueling, then why was L2 selected as its location?  There are several reasons, all related to the scientific objectives of JWST.

Less Interference from Earth

The JWST is an infrared telescope, meaning it will use the infrared part of the spectrum to snap photos of distant objects in space. Therefore, any thermal interference, in the form of infrared radiation, is a major impediment to the function of JWST’s infrared detectors.

The Earth itself is a major radiator of infrared radiation. For an instrument as sensitive as the JWST, the Earth would be like a bright infrared beacon in the night. Getting the telescope far from the Earth will reduce the impact of Earth’s infrared output.

Shielded from the Sun

Because warm bodies emit infrared radiation, the JWST instruments themselves need to be cold enough that their own infrared emission won’t interfere with its ultra-sensitive infrared sensors.

“Warm” is relative, so what counts as warm? A quick application of Wien’s Displacement Law (which can be done easily using an online calculator like this one) tells us that a body’s thermal spectrum will peak in the infrared (700 nm to 1 mm wavelengths) at temperatures between about -270 °C and about +4000 °C. Ideally the JWST’s temperature would lie outside this range, and since +4000 °C is hot enough to melt any metal, then we want to be at the other end of the range. So the JWST should be as close to -270 °C as possible so that its own infrared emission won’t interfere with its instruments.

On top of this, the Stefan-Boltzmann Law tells us that as the temperature goes down, the total thermal radiation output goes down dramatically (as the fourth power of temperature).

Bottom line: the colder, the better.

To accomplish this, the JWST has a giant sun shield that will protect it from the Earth’s and — especially — the Sun’s radiation.

Being at L2, where it orbits in lock-step with the Earth and it has both the Earth and Sun always on the same side, JWST’s sun shield will automatically stay positioned between the telescope and those two dominant sources of radiation.

The expected temperatures on each side of the sun shield are about -240 °C (-400 °F) for the telescope side (pretty close to the estimate of -270 °C using Wien’s Law) and 93 °C (200 °F) for the side facing the Earth and Sun.

No Obstruction of View

The Hubble Space Telescope orbits the Earth once about every 95 minutes. This means that for 47.5 minutes during each orbit the Earth will be positioned between Hubble and deep space. For half of the time that the Hubble mission has been ongoing, the Earth blocks its view.

Not only does this divide the usable deep space observation time of Hubble in half, it also limits the maximum exposure length that Hubble can use for taking a photo to 47.5 minutes.

By putting JWST at L2, however, it is not orbiting the Earth and the Earth will never obstruct its view of deep space. This allows the JWST to take images during 100% of its mission time. And, perhaps most importantly, there is no upper limit to the exposure length for taking an image. Having this unlimited exposure time will allow JWST to use very long exposure times to image extraordinarily faint objects that previously couldn’t be imaged.

Minimal Fuel Consumption

As mentioned above, in order to maintain its orbit around L2, the JWST will only have to burn fuel once every three weeks. This is a modest amount of fuel usage, much less than would be needed to stay in certain low Earth orbits, like that of the ISS. Therefore, although it will be out of reach by current and near-future spacecraft for refueling, its fuel consumption will be minimal and that will allow its fuel to last for up to a decade, hopefully.

Conclusion

JWST’s mission will involve imaging distant galaxies that formed 13.6 billion years ago as well as peering into the atmospheres of tiny, distant, and extremely dim planets outside our solar system.  These feats wouldn’t be possible without the advantages that are afforded by its positioning at L2.

Further Information:

This YouTube video offers a great explanation of Lagrange Points, including some nice 3D visualizations of the potential field that results when you combine gravitational and centrifugal forces: What Makes Lagrange Points Special Locations In Space

This article from astronomy.com also provides a nice summary of the reasons for placing JWST at L2: James Webb Space Telescope will carry out science from a special spot.

Note: The astronomy.com article mistakenly uses the centripetal force to describe Lagrange points instead of the centrifugal force. This is a common mistake because (a) centripetal and centrifugal forces are equal (but opposite) and (b) centripetal force is not “fictitious” like centrifugal force is. Therefore, it’s commonly thought that centripetal force is the only “real” force that can be talked about. But as I described above, centrifugal forces are definitely “real”, in that they can be felt; centrifuges work just fine!