How Long Will It Last?

Using the Copernican Principle to predict the future lifespan of just about anything
Mark Baumann
May 26, 2024
In 1993, Princeton astrophysicist J. Richard Gott published a paper [1]Gott, J.R. Nature 363 (1993): 315-319 “Implications of the Copernican Principle for Our Future Prospects” in the journal Nature in which he used the Copernican Principle to predict the future lifespan of a variety of things, ranging from the Berlin Wall to the human species as a whole.
I find his argument extremely interesting and want to share the idea in this article. Before we apply the Copernican Principle, let’s discuss what the Copernican Principle is.
The Copernican Principle
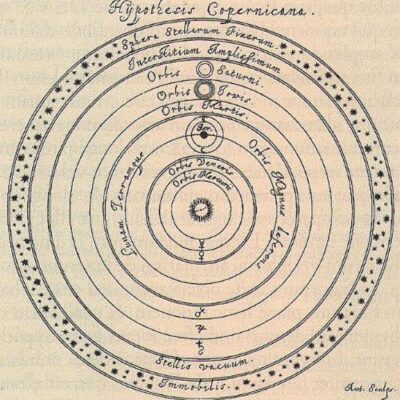
In 1543, Copernicus proposed that the Sun is at the center of the solar system
In 1543, Nicolaus Copernicus published his book “On the Revolutions of Heavenly Spheres” in which he proposed that the planets revolve around the Sun (heliocentrism) rather than around the Earth (geocentrism). [2]Greek astronomer Aristarchus may have been the first to propose a heliocentric model of the solar system. In addition to this, he correctly predicted that the stars were other suns that are much … Continue reading Copernicus also correctly proposed that the Earth rotates on its axis once each day.
This initiated the Copernican Revolution — a period that started with the publication of Copernicus’s book and lasted about a century — during which the prevailing worldview transitioned from a geocentric model of our solar system to a heliocentric model. It wasn’t a smooth transition; infamously, Galileo was declared a heretic by the Catholic Church and placed under house arrest for the rest of his life for his support of the idea that the Earth wasn’t at the center of the cosmos.
One of the key lessons we learned from this transition is that humanity does not occupy a privileged position at the center of the universe. What we observe here on Earth should not be special to us but should be representative of observations made elsewhere in the universe. Our place in the universe is normal, not special.
In the words of Nobel Laureate Steven Weinberg: “Ever since Copernicus we have learned to beware of supposing there is anything special about mankind’s location in the universe.” [3]Weinberg, Steven. The First Three Minutes. (Perseus Books Group, New York, 1977).
This heuristic has been dubbed the Copernican Principle.
The Copernican Principle and Modern Cosmology
The Copernican Principle plays a key role in modern day cosmology (the study of the universe). Astronomical observations by Hubble and others in the 1920’s revealed that distant galaxies are moving away from us. Moreover, the rate of the recession of a galaxy is proportional to the distance to that galaxy. This observation has been named Hubble’s Law.
Interestingly, no matter in what direction you look, all distant galaxies appear to be moving away from us.
Does that mean we’re at the center of the universe and everything is moving away from a special, central point that’s occupied by us? Applying the Copernican Principle, the answer must be: no!
What we see should match what other observers in other galaxies would see. In other words, observers at every point in the universe should see every distant galaxy moving away from them.
How is it possible that every observer in every galaxy would see every other galaxy moving away from them? It would imply that the universe is expanding like a stretching rubber sheet.
Again, from Steven Weinberg: “Other galaxies are generally rushing away from our own. Of course, this does not mean that our galaxy has any special central position. Rather, it appears that the universe is undergoing some sort of explosion in which every galaxy is rushing away from every other galaxy… every pair of galaxies is moving apart at a relative speed proportional to their separation.” [4]Weinberg, Steven. The First Three Minutes. (Perseus Books Group, New York, 1977).
In other words, if Hubble’s Law is true for observers in our galaxy, it must also be true for observers in every other galaxy.
Indeed, you can do a careful tabletop experiment with a rubber band to confirm that all points on a stretching rubber band obey Hubble’s Law. It’s an assignment in my astronomy class to reproduce Hubble’s Law by tracking points along a one-dimensional expanding model in the classroom. If you’d like to try it yourself, you can download the lesson here.
These observations and realizations eventually led to the Big Bang Model. An additional prediction of the Big Bang Model is that there should be a leftover radiation signature from the hot, early stage of the universe. And this prediction was verified with the discovery in 1964 of the Cosmic Microwave Background (CMB). As Gott describes the discovery of the CMB: “This remains one of the most remarkable predictions to be verified in the history of science –- all because of taking seriously the idea that your location is not special.” [5]Gott, J. Richard. Time Travel in Einstein’s Universe. (First Mariner Books, New York, 2001)
As a guiding principle, the Copernican Principle has served us extraordinarily well.
Our Place In Time
Gott published a paper in Nature in 1993 that proposed a brilliant variation on how we can apply the Copernican Principle. So far, we’ve been applying the Principle to our place in space: humans don’t occupy the center of the solar system (Copernicus) or of the galaxy (our solar system is about 28,000 light years from the galactic center) or of the universe (Hubble).
Gott asked: what if we applied the Copernican Principle to our place in time? As observers, we may not occupy a special place in time, just like we don’t occupy a special place in space. What can we do with that realization?
Gott’s first application of this idea came when he was visiting the Berlin Wall in 1969 and he asked himself how much longer the wall would remain standing. At that time the wall had been standing for 8 years. Many people thought the wall would be temporary while many others thought it would become a permanent fixture in Berlin.
Gott started with the assumption that he wasn’t visiting the wall at any particularly special time in its history. He wasn’t witnessing the building of the wall and he wasn’t witnessing the tearing down of the wall. If he wasn’t there at any particularly special time, then it was just as likely that he was visiting the wall at one moment in its existence as at any other moment in its existence. He could be visiting the wall at the 1/4 point of its lifespan, or the halfway point, or the 2/3 point, etc… the likelihood of each is the same.
Therefore, one can conclude there was a 50% chance that he was visiting the wall during the middle 50% of its lifespan. Why the middle? Because we are working on the assumption that he wasn’t visiting the wall at the beginning (i.e., the building) of the wall nor the ending (i.e., the tearing down) of the wall.
If he’s in the middle 50% of its lifespan, then at least 25% of its life has already passed and at least 25% of its lifespan has yet to pass (see figure).
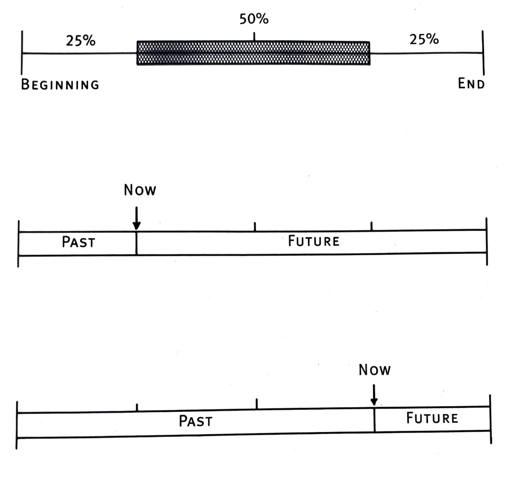
If we’re witnessing something during the middle 50% of its lifespan (top), then at the earliest we are 25% of the way into its life with 75% left to go (middle) and at the latest we are 75% of the way into its life with 25% left to go (bottom). [Image from Gott’s book, Time Travel in Einstein’s Universe [6]Gott, J. Richard. Time Travel in Einstein’s Universe. (First Mariner Books, New York, 2001)]
At the latest, he’s visiting the wall when it has only 25% of its life remaining. Being 8 years old, that means three-quarters of the wall’s life equals 8 years, and the remaining quarter is 8/3 years or (rounding off) about 3 years.
Therefore, Gott concluded, there was a 50% chance that the Wall would last between 3 and 24 more years. The Wall came down in 1989, 20 years after his visit, which confirmed his prediction.
Note that we’ve said nothing about how or why the wall would end. We simply estimated its future life expectancy based on the fact that we are not observing it at any special time in its lifespan.
It’s a simple and brilliant application of the Copernican Principle.
Broadening the Interval
We’ve made a prediction that will come true 50% of the time, but scientific rigor conventionally demands at least 95% confidence in any prediction. The same Copernican Principle argument can be applied for any confidence interval. For instance, obviously we can say with 100% confidence that we are present during the middle 100% of the lifespan of something that we are witnessing.
Now let’s try applying the Copernican Principle using a 95% confidence interval. We’ll use the Internet as an example.
How much longer will the Internet last? Using the same argument as above, there is a 95% chance that we are in the middle 95% of the Internet’s lifespan (see figure).
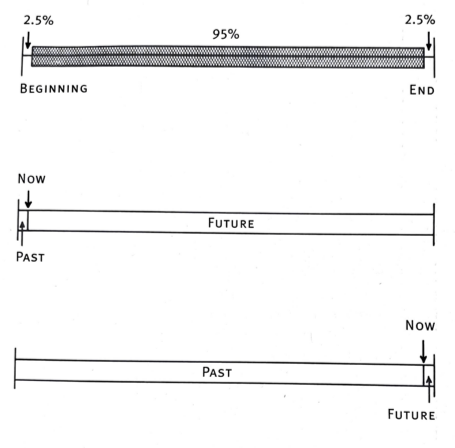
If we’re witnessing something during the middle 95% of its lifespan (top), then at the earliest we are 2.5% of the way into its life with 97.5% left to go (middle) and at the latest we are 97.5% of the way into its life with 2.5% left to go (bottom). [Image from Gott’s book, Time Travel in Einstein’s Universe [7]Gott, J. Richard. Time Travel in Einstein’s Universe. (First Mariner Books, New York, 2001)]
At the latest, there is only 2.5% of its life to go. That means the Internet has lived 39/40 of its life and has just 1/40 to go. So, at the other extreme, its future lifespan is 1/39 times its current age (since 39/40 times 1/39 is 1/40).
In summary, to use the Copernican Principle with 95% confidence, we need to multiply and divide the Internet’s current age by 39 to get the upper and lower limits on its future lifespan. Let’s call this the Rule of 39.
Now we need to determine how old the Internet currently is. This in itself is an interesting question. The Internet didn’t just spring up fully formed; its creation was a gradual process over the course of numerous inventions. So its birthdate is debatable. I’ll take January 1, 1983 as the birth of the Internet since that was the date of the adoption of the TCP/IP protocol, which allowed computers of all kinds to communicate between separate networks. That places the age of the Internet at 41 years old.
Applying the Rule of 39 to the Internet’s age of 41 years means it has at minimum another 1.1 more years to exist (41 divided by 39) and at most about 1600 more years to exist (41 times 39). That’s an extremely broad interval, but that’s what we should expect because we are saying this with 95% confidence.
It’s interesting that we can say, just by assuming that we are not special observers and we are not at a special point in time, that there is a 95% chance that the Internet won’t last beyond 1600 more years. Compared to the length of recorded history so far (about 5000 years), the Internet will last much less time than writing has been around. Of course, we are saying nothing about what will cause the Internet’s demise, or what will replace it. But we need not know this information in order to apply the Copernican Principle.
The 50% confidence interval for the future lifespan of the Internet is at least 14 years and at most 123 years. The upper bound of this interval (123 years) is significantly smaller than the upper bound of the 95% confidence interval (1600 years). The difference of nearly 1500 years is needed just to cover the additional 45% that brings us up to 95% confidence, whereas a simple 50% confidence requires a mere 123 years. From this we can conclude that the upper bound of the 95% interval will, in many cases, far exceed the actual lifespan of something. So it’s worth noting that we can also use the 50% confidence interval, which is significantly smaller, and still be right 50% of the time.
The Copernican Principle applied to time has a built-in feature: the longer something has lasted so far, the longer we expect it to continue lasting. This is also known as Lindy’s Law, which states that the future life expectancy of something is proportional to its current age. [8]Eliazar, Iddo. “Lindy’s Law”. Physica A: Statistical Mechanics and Its Applications. 486: 797–805 (2017).
It’s important to emphasize again that the Copernican Principle only applies in cases where the observer does not occupy a special place in time. If you are present for the birth of something, then you are observing it at a special place in its lifespan. Take, for example, attending a wedding. As Gott admonishes: “one minute after the vows are finished [don’t] proclaim that the marriage has less than 39 more minutes to go.” [9]Gott, J. Richard. Time Travel in Einstein’s Universe. (First Mariner Books, New York, 2001) The Copernican Principle simply doesn’t work in this case because it doesn’t apply if you are witnessing a special moment in something’s lifespan, such as the beginning or end.
It’s also worth mentioning again that I’m not saying anything with 100% certainty. The only thing that can be said with 100% certainty is that the future lifespan of something lies between 0 and infinite more years.
Let’s look at a few more applications of the Copernican Principle.
How long will the human species last?
The age of the human species (Homo sapiens) is about 200,000 years, according to an analysis done by Cann, Stoneking, and Wilson. [10]Cann, Stoneking, and Wilson. “Mitochondrial DNA and human evolution”. Nature 325 (1987): 31. In their analysis, the authors used mitochondrial DNA to trace the ancestors of people from five distinct geographic regions around the world back to a single ancestor who lived 200,000 years ago in Africa.
Applying the Rule of 39 gives the following interval for the remaining lifespan of the human race: at least 5,128 more years and no more than 7,800,000 more years. Adding the current age of 200,000 years gives a total lifespan for Homo sapiens between about 0.2 million years and 8 million years.
Homo sapiens and archaic humans [image credit: Encyclopedia Britannica]
It’s fascinating that the Copernican Principle predicts a lifespan of the human species that falls within these expected values. One might argue that, as a highly intelligent species, we should be able to lengthen the lifespan of our species through medicine, genetic engineering, bionics, space colonization, etc. On the other hand, with such advancements also come technologies that pose existential threats, such as nuclear weapons. Furthermore, we are subject to the same epidemic and ecological disasters (including asteroid impacts) as the rest of the species on Earth. So perhaps it’s reasonable that our life expectancy is in the same ballpark as that of other species on Earth.
How long will civilization last?
The beginning of civilization was characterized by a transition from nomadic hunter-gatherers to a stationary lifestyle dependent upon agriculture for sustenance – the agricultural revolution. This in turn led to urbanization, economics, architecture, and writing. Therefore, for our purposes here I’ll take the appearance of the earliest cities as the beginning of civilization.

Current excavation of Çatalhöyük [image credit: UNESCO]
Therefore, let’s take 9,500 years as the age of civilization. Applying the Rule of 39 gives the remaining lifespan of civilization to be between 244 years and 370,500 years. Add to that the current 9,500-year age of civilization and that gives a total lifespan of between 9,744 years and 380,000 years. The upper limit of 380,000 years is a very long time, but it is also notably smaller than the average age of mammal species (2 million years) and insignificant compared to the age of the Earth (4.5 billion years).
Comparing the upper limit of civilization’s lifespan (380,000 years) to the upper limit of homo sapiens’ lifespan (8 million years), it is reasonable to conclude that the human species will likely outlast civilization itself. This implies the eventual demise of civilization and a return to the hunter-gatherer lifestyle sometime in our future.
How many people will live?
How many human beings will ultimately live on planet Earth? Current estimates suggest that 117 billion people have lived on Earth so far. [14]https://www.prb.org/articles/how-many-people-have-ever-lived-on-earth/ Therefore, you are roughly the 117 billionth person on Earth. The Copernican Principle suggests that your status as the 117 billionth person is not a special status in the history of the human race. As pointed out by physicist Holgar Nielsen in a paper published in Acta Physica Polonica [15]Nielsen, H.B. Acta Physica Polonica B20 (1989): 427., you should expect to be located randomly on the chronological list of all human beings.
We can apply the Rule of 39 to the number of people that have lived on Earth so far to find out how many more might ultimately live. Dividing and multiplying by 39 gives at least 3 billion more people and no more than 4.6 trillion more people.
Notice that this statement alone predicts, with 95% certainty, that the human race will not last forever. Indeed, we’ve already calculated – using the Rule of 39 – that the human race likely will not survive beyond another 7.8 million years.
There’s another way to see that the human race probably will not be extremely long-lived. Suppose for the sake of argument that it will last forever. Then, a trillion years from now, for example, the human race would still exist. At that point in time, the age of the human race (slightly more than a trillion years) would nearly equal the age of the universe (about 1% more than a trillion years). And that would also be true for the infinite number of humans that will come after that. So, if humans lasted forever, it would be very likely that we’d be alive at a time when the past history of human beings is almost as old as the age of the universe. But we live at a time where the age of the universe (13.7 billion years) is much larger than the age of the human race (200,000 years). That would put us incredibly close to the beginning of the infinitely-long lifespan of our species, and that would make us incredibly special. But, according to the Copernican Principle, it is very unlikely that we are so special.
The population curves of all species through time look similar: the population starts small, grows to some maximum, then diminishes until the species goes extinct. As discussed, it’s likely that the human race will experience the same and eventually go extinct. When in the history of the human race do we live? We likely live near the peak, because that’s where most people in history will live.
Do we live at a special time in the history of the human race since we live in an age of discovery? Gott argues that we shouldn’t be surprised that we live in an age of discovery. We likely live at a time when humans are near their peak in population and, since it is people that make discoveries, then living at a time of peak population would also entail living in an age of discovery. Therefore, it is probable we would live in an age of discovery.
Will the human race become spacefaring?

Scale model of Vostok 1, Yuri Gagarin’s spacecraft [image credit: Smithsonian National Air and Space Museum]
A trip to our nearest neighboring star, Proxima Centauri, traveling at the speed of our fastest-ever spacecraft (the Parker Solar Probe), would take over 7,800 years – significantly longer than the 2,457-year upper limit on human space travel. This indicates we will likely need to find technology to convey humans faster than current rocket technology if we are going to become a spacefaring species. I have a series of four articles on this subject if you’d like to read more.
In another article, I presented a prediction that if vehicle speeds continue improving at their current rate, the optimal time to wait before beginning our trip to Proxima Centauri is about 176 years. Some good news is that this falls well within the 95% confidence interval, and even just barely within the much smaller 50% confidence interval (which is 21 years to 189 years).
Could the human race eventually become a supercivilization that colonizes the entire galaxy? According to the Copernican Principle, likely not. As Gott points out: “The fraction of civilizations like ours that eventually turn into supercivilizations with their enormous populations must be extremely low; otherwise, you would likely be sitting in one right now.”
Summary and Further Reading
In the table below, I’ve summarized the expected lifespans of things we’ve discussed in this article. I’ve included both the 50% and 95% confidence intervals.
Feel free to compute your own intervals for something you are interested in. Applying the Copernican Principle is easy. To find the 95% interval, use the Rule of 39: take the current age of something and divide by 39 for the lower estimate of its remaining lifespan, and multiply by 39 for the upper estimate. Using 95% confidence means: if you make 100 predictions, about 95 of your predictions will prove accurate and 5 of them will not.
If you’d like to find the much smaller 50% confidence interval (in which about half of your predictions should prove accurate), you can apply the Rule of 3: divide the current age by 3 for the lower estimate and multiply by 3 for the upper estimate.
For much more discussion of applying the Copernican Principle to time, including these topics as well as the lifespan of things like political parties, Broadway shows, dictatorships, the Soviet Union, the Seven Wonders of the World, ocean liners, and space colonization, I recommend checking out the final chapter of J. Richard Gott’s book: Time Travel in Einstein’s Universe. [16]Gott, J. Richard. Time Travel in Einstein’s Universe. (First Mariner Books, New York, 2001)
| Age | Min Time Remaining
(50% conf) |
Max Time Remaining
(50% conf) |
Min Time Remaining
(95% conf) |
Max Time Remaining
(95% conf) |
|
|---|---|---|---|---|---|
| Human species | 200,000 yrs | 67,000 yrs | 600,000 yrs | 5,128 yrs | 7,800,000 yrs |
| Civilization | 9,500 yrs | 3,167 yrs | 28,500 yrs | 244 yrs | 370,500 yrs |
| United States | 248 yrs | 83 yrs | 744 yrs | 6 yrs | 9,672 yrs |
| Human spaceflight | 63 yrs | 21 yrs | 189 yrs | 2 yrs | 2,457 yrs |
| Internet | 41 yrs | 14 yrs | 123 yrs | 1 yr | 1,599 yrs |
Footnotes
| ↑1 | Gott, J.R. Nature 363 (1993): 315-319 “Implications of the Copernican Principle for Our Future Prospects” |
|---|---|
| ↑2 | Greek astronomer Aristarchus may have been the first to propose a heliocentric model of the solar system. In addition to this, he correctly predicted that the stars were other suns that are much farther away. He lived circa 310 BCE to 230 BCE. |
| ↑3, ↑4 | Weinberg, Steven. The First Three Minutes. (Perseus Books Group, New York, 1977). |
| ↑5, ↑6, ↑7, ↑9, ↑12, ↑16 | Gott, J. Richard. Time Travel in Einstein’s Universe. (First Mariner Books, New York, 2001) |
| ↑8 | Eliazar, Iddo. “Lindy’s Law”. Physica A: Statistical Mechanics and Its Applications. 486: 797–805 (2017). |
| ↑10 | Cann, Stoneking, and Wilson. “Mitochondrial DNA and human evolution”. Nature 325 (1987): 31. |
| ↑11 | Stanley, S.M. “A theory of evolution above the species level”. Proceedings of the National Academy of Sciences 72 (1975): 646-650. |
| ↑13 | https://en.wikipedia.org/wiki/History_of_cities#Mediterranean_and_Mesopotamia |
| ↑14 | https://www.prb.org/articles/how-many-people-have-ever-lived-on-earth/ |
| ↑15 | Nielsen, H.B. Acta Physica Polonica B20 (1989): 427. |
